Unidad 4: Tipos de Arboles

Arboles binarios:

son árboles donde cada nodo sólo puede apuntar a dos nodos

Se define un árbol binario como un conjunto finito de elementos (nodos) que bien esta vacío o esta formado por una raíz con dos arboles binarios disjuntos, es decir, dos descendientes directos llamados subarbol izquierdo y subarbol derecho.

Los árboles binarios (también llamados de grado 2 )tienen una especial importancia.

Las aplicaciones de los arboles binarios son muy variadas ya que se les puede utilizar para representar una estructura en la cual es posible tomar decisiones con dos opciones en distintos puntos.

ARBOLES BINARIOS DE BUSQUEDA

Son árboles binarios ordenados. Desde cada nodo todos los nodos de una rama serán mayores, según la norma que se haya seguido para ordenar el árbol, y los de la otra rama serán menores.

Los árboles binarios se utilizan frecuentemente para representar conjuntos de datos cuyos elementos se identifican por una clave única. Si el árbol está organizado de tal manera que la clave de cada nodo es mayor que todas las claves su subárbol izquierdo, y menor que todas las claves del subárbol derecho se dice que este árbol es un árbol binario de búsqueda.

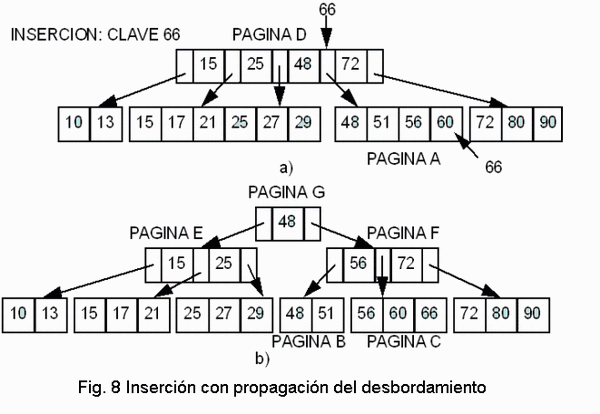
ARBOLES- B

Son árboles cuyos nodos pueden tener un número múltiple de hijos tal como muestra el esquema.

Unidad 4: Recorrido Arbol

Existen dos recorridos típicos para listar los nodos de un árbol: primero en profundidad y primero en anchura.

 En el primer caso, se listan los nodos expandiendo el hijo actual de cada nodo hasta llegar a una hoja, donde se vuelve al nodo anterior probando por el siguiente hijo y así sucesivamente. En el segundo, por su parte, antes de listar los nodos de nivel n + 1 (a distancia n + 1 aristas de la raíz), se deben haber listado todos los de nivel n. Otros recorridos típicos del árbol son:

El recorrido en preorden, también llamado orden previo consiste en recorrer en primer lugar la raíz y luego cada uno de los hijos  en orden previo

El recorrido en inorden, también llamado orden simétrico (aunque este nombre sólo cobra significado en los árboles binarios) consiste en recorrer en primer lugar A₁, luego la raíz y luego cada uno de los hijos   en orden simétrico

El recorrido en postorden, también llamado orden posterior consiste en recorrer en primer lugar cada uno de los hijos   en orden posterior y por último la raíz.

PREORDEN	INORDEN	POSORDEN
Raíz	Hijo izquierdo	Hijo izquierdo
Hijo izquierdo	Raíz	Hijo derecho
Hijo derecho	Hijo derecho	Raíz

Unidad 4: Arboles y Caracteristicas

Los árboles son estructuras de datos no lineales.

Cada elemento conocido con el nombre de NODO

Un árbol se define como una colección de nodos donde cada uno además de almacenar información, guarda las direcciones de sus sucesores.  

Se conoce la dirección de uno de los nodos, llamado raíz y a partir  de el se tiene acceso a todos los otros miembros de la estructura.

Grafos, anidación de paréntesis y diagramas de venn.  

Hijo: Es aquel nodo que siempre va a tener un nodo antecesor o padre, son aquellos que se encuentran en el mismo nivel  

Padre: Es aquel que tiene hijos y también puede tener o no antecesores.  

Hermano: Dos nodos son hermanos si son apuntados por el mismo nodo, es decir si tienen el mismo padre.  

Raíz: Es el nodo principal de un árbol y no tiene antecesores.   

Hoja o terminal: Son aquellos nodos que no tienen hijos o también los nodos finales de un árbol. 

Interior: Se dice que un nodo es interior si no es raíz ni hoja. 

Nivel de un nodo: Se dice que el nivel de un nodo es el numero de arcos que deben ser recorridos, partiendo de la raíz para llegar hasta el. 

Altura del árbol: Se dice que la altura de un árbol es el máximo de los niveles considerando todos sus nodos. 

Grado de un nodo: se dice que el grado de un nodo es el número de hijos que tiene dicho nodo.

Unidad 4: Representacion en Programas

REPRESENTACION DE LOS GRAFOS EN PROGRAMAS

Representación mediante matrices:   

La forma másfácil de guardar la información de los nodos esmediante la utilización de un vector que indexe losnodos, de manera que los arcos entre los nodos se pueden ver como relaciones entre los índices. Esta relación entre índices se puede guardar en unamatriz, que llamaremos de adyacencia

Representación mediante listas:    

En las listas de adyacencia lo que haremos será guardar por cada nodo, además de la información que pueda contener el propio nodo, una lista dinámica con los nodos a los que se puede acceder desde él. La información de los nodos se puede guardar en un vector, al igual que antes, o en otra lista dinámica

Representación mediante matrices dispersas:  
Para evitar uno de los problemas que teníamos con las listas de adyacencia, que era la dificultad de obtener las relaciones inversas, podemos utilizar las matrices dispersas, que contienen tanta información como las matrices de adyacencia, pero, en principio, no ocupan tanta memoria como las matrices, ya que al igual que en las listas de adyacencia, sólo representaremos aquellos enlaces que existen en el grafo

Unidad 4: Clasificacion de Grafos

Los grafos se pueden clasificar en dos grupos:

 Dirigidos y no Dirigidos.

En un grafo dirigido cada arco está representado por un par ordenado de vértices, de forma que  representan dos arcos diferentes

En un grafo no dirigido el par de vértices que representa un arco no está ordenado

TIPOS DE GRAFOS 

Grafo regular: Aquel con el mismo grado en todos los vértices

Grafo bipartito: Es aquel con cuyos vértices pueden formarse dos conjuntos disjuntos de modo que no haya adyacencias entre vértices pertenecientes al mismo conjunto

Grafo completo: Aquel con una arista entre cada par de vértices

Grafo nulo: Se dice que un grafo es nulo cuando los vértices que lo componen no

están conectados, esto es, que son vértices aislado

Grafos Isomorfos: Dos grafos son isomorfos cuando existe una correspondencia

biunívoca (uno a uno), entre sus vértices de tal forma que dos de estos quedan

unidos por una arista en común

      

Grafos Platónicos: Son los Grafos formados por los vértices y aristas de los cinco sólidos regulares (Sólidos Platónicos), a saber, el tetraedro, el cubo, el octaedro, el dodecaedro y el icosaedro

     

Grafo conexo

Un grafo se puede definir como conexo si cualquier vértice V pertenece al conjunto

de vértices y es alcanzable por algún otro. Otra definición que dejaría esto más

claro sería: “un grafo conexo es un grafo no dirigido de modo que para cualquier

par de nodos existe al menos un camino que los une” 

DÍGRAFO (GRAFO DIRIGIDO).

A un grafo dirigido se le puede definir como un grafo que contiene aristas dirigidas,

como en el siguiente caso